1. 공분산(Covariance) ㅇ 두 변량(확률변수 등) 사이에 상관성/의존성/유사성의 방향 및 정도에 대한 척도 ※ [참고] - 상관성 의미 ☞ 상관(Correlation) 참조 - 공분산 행렬 ☞ 확률벡터 참조 2. 공분산 및 상관(계수) 정의 ㅇ 공분산 (Covariance) - 두 변량이 상관적으로 변화되는 척도 . 두 변량이 각각의 평균으로부터 변화하는 방향 및 양에 대한 기대값 .. 보통 Cov(X,Y),σXY로 표시함ㅇ 상관 계수 (Correlation Coefficient) = 정규화된 공분산 - 공분산이 각 변량의 단위에 의존하게되어 변동 크기량이 모호하므로, 공분산에다가 각 변량의 표준편차를 나누어주어 `정규화`시킴
. 여기서, Var() : 분산, σX : 표준편차, Cov(X,Y) : 공분산 - 특징 . 단위가 무차원(dimensionless)임 . -1 ≤ ρXY ≤ 1 3. 공분산 또는 상관계수 값에 따른 의미 ㅇ 양수 : `강한 양의 상관관계` (positively correlated) - 두 변량이 같은 방향으로 움직임 (X가 커지면 Y도 덩달아 커짐) ㅇ 음수 : `강한 음의 상관관계` (negatively correlated) - 두 변량이 반대방향으로 움직이는 것 (X가 커지면 Y는 작아짐) ㅇ 0(영) : `상관관계 없음` (uncorrelated) - 두 변량 간에 직선적인 혹은 비례적인 관계를 발견할 수 없을 때를 말함 . 즉, 통계적 독립인 경우 임 :
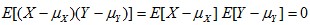
4. 공분산 성질 ㅇ 교환법칙 :
ㅇ 동일 변량에 대한 공분산은 분산이 됨 :
ㅇ 기타성질
5. 다변량 확률변수의 공분산 ※ ☞ 공분산 행렬 참조 - 2 변량 이상의 변량이 있는 경우에 모든 변량 쌍들 간의 공분산을 행렬로 표현한 것
출처: http://www.ktword.co.kr/abbr_view.php?m_temp1=2890
'경제&금융' 카테고리의 다른 글
| 2018 수정된 양도세와 종부세 정리 (0) | 2018.07.13 |
|---|---|
| 전세계 완성차 시가총액 및 밸류에이션 (0) | 2017.06.15 |
| 성광벤드(2017-02-21-KB) 리포트 (0) | 2017.02.21 |
| CDO와 합성CDO의 차이 (0) | 2017.02.15 |
| CDS와 CLN의 차이 (0) | 2017.02.15 |



